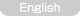正解は左図のように歯車を置きます。
この問題のポイントは歯車の歯数と歯車の個数にあります。
それは、歯車の歯数が回転数、歯車の個数が回転方向に関係しているからです。

まずは歯車の歯数について考えます。

異なる回転数で回転させるためには２つの歯車の歯数を同じにしてはいけません。
この問題の場合、40・ギアと24・ギアを使用しているため、40・ギアが1回転すると24ギアは約1.7回転します。

これは左図のように
駆動側の歯車の歯数÷従動側の歯車の歯数
の計算で、駆動側と従動側の比率を求めることでわかります。

次に歯車の個数について考えます。
歯車を使用する場合、隣り合う歯車の回転方向は必ず逆向きになります。

実際に動かした様子はこちら
この動画は、左側の歯車を時計回りに回転させています。
手で左側の歯車を回して、右側の歯車の様子を確認してみましょう。

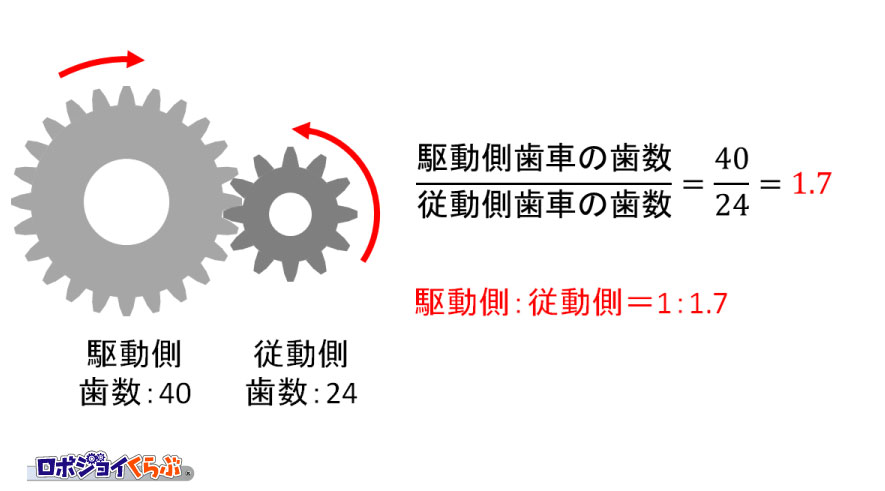
正解は左図のように3つの歯車を置きます。

この問題のポイントは(1)と同じです。
隣り合う歯車の回転方向は歯車の数と関係しているので、
偶数 (2・4・6・・・) 個：逆方向
奇数 (3・5・7・・・) 個：同じ方向
となります。

また、同じ回転数で回転させるために、同じ歯数の歯車を使います。

この問題の場合、40・ギアと24・ギアと40・ギアを使用しているので、その中からまず左側の2つの歯車を考えます。
40・ギアが1回転すると24・ギアは約1.7回転します。

次に右側の2つの歯車を考えます。
24・ギアが1.7回転すると40・ギアは1回転します。

左図のように40・ギアを置き、左側を駆動側とし、右側を従動側とします。

駆動側の歯車を時計回りに1回転すると、
従動側の歯車が反時計回りに0.5回転するには、
間にどのように歯車を配置すればいいでしょうか？